Der Radius einer Kugel (abgekürzt als die Variable r oder R) ist der Abstand vom exakten Mittelpunkt der Kugel zu einem Punkt an der Außenkante dieser Kugel. Wie bei Kreisen ist der Radius einer Kugel oft ein wesentlicher Teil der Anfangsinformation zum Berechnen des Durchmessers, des Umfangs, der Oberfläche und / oder des Volumens der Form. Sie können jedoch auch rückwärts von Durchmesser, Umfang usw. arbeiten, um den Radius der Kugel zu finden. Verwenden Sie die Formel, die mit den Informationen funktioniert, die Sie haben.
Methode eins von dreien:
Verwenden von Radiusberechnungsformeln
-
 1 Finde den Radius, wenn du den Durchmesser kennst. Der Radius ist der halbe Durchmesser. Verwenden Sie die Formel r = D / 2. Dies ist identisch mit der Methode, mit der der Radius eines Kreises aus seinem Durchmesser berechnet wird.[1]
1 Finde den Radius, wenn du den Durchmesser kennst. Der Radius ist der halbe Durchmesser. Verwenden Sie die Formel r = D / 2. Dies ist identisch mit der Methode, mit der der Radius eines Kreises aus seinem Durchmesser berechnet wird.[1] - Wenn Sie eine Kugel mit einem Durchmesser von 16 cm haben, finden Sie den Radius, indem Sie 16/2 teilen, um zu erhalten 8 cm. Wenn der Durchmesser 42 ist, dann ist der Radius 21.
-
 2 Finde den Radius, wenn du den Umfang kennst. Verwende die Formel C / 2 & pgr ;.. Da der Umfang gleich πD ist, was gleich 2πr ist, ergibt die Division des Umfangs durch 2π den Radius.[2]
2 Finde den Radius, wenn du den Umfang kennst. Verwende die Formel C / 2 & pgr ;.. Da der Umfang gleich πD ist, was gleich 2πr ist, ergibt die Division des Umfangs durch 2π den Radius.[2] - Wenn Sie eine Kugel mit einem Umfang von 20 m haben, finden Sie den Radius durch Division 20 / 2π = 3,183 m.
- Verwenden Sie die gleiche Formel, um zwischen dem Radius und dem Umfang eines Kreises zu konvertieren.
-
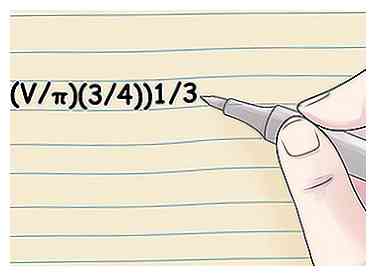 3 Berechnen Sie den Radius, wenn Sie das Volumen einer Kugel kennen. Benutze die Formel ((V / π) (3/4))1/3.[3] Das Volumen einer Kugel ergibt sich aus der Gleichung V = (4/3) πr3. Die Lösung für die r-Variable in dieser Gleichung erhält ((V / π) (3/4))1/3 = r, was bedeutet, dass der Radius einer Kugel gleich dem Volumen dividiert durch π, mal 3/4 ist, alle zu der Potenz 1/3 (oder der Kubikwurzel).[4]
3 Berechnen Sie den Radius, wenn Sie das Volumen einer Kugel kennen. Benutze die Formel ((V / π) (3/4))1/3.[3] Das Volumen einer Kugel ergibt sich aus der Gleichung V = (4/3) πr3. Die Lösung für die r-Variable in dieser Gleichung erhält ((V / π) (3/4))1/3 = r, was bedeutet, dass der Radius einer Kugel gleich dem Volumen dividiert durch π, mal 3/4 ist, alle zu der Potenz 1/3 (oder der Kubikwurzel).[4] - Wenn Sie eine Kugel mit einem Volumen von 100 Zoll haben3, löse den Radius wie folgt:
- ((V / π) (3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31.83)(3/4))1/3 = r
- (23.87)1/3 = r
- 2.88 in = r
- Wenn Sie eine Kugel mit einem Volumen von 100 Zoll haben3, löse den Radius wie folgt:
-
 4 Finde den Radius von der Oberfläche. Verwende die Formel r = √ (A / (4π)). Die Oberfläche einer Kugel ergibt sich aus der Gleichung A = 4πr2. Das Auflösen für die r-Variable ergibt √ (A / (4π)) = r, was bedeutet, dass der Radius einer Kugel gleich der Quadratwurzel der Oberfläche dividiert durch 4π ist. Sie können auch (A / (4π)) für das gleiche Ergebnis auf die halbe Potenz bringen.[5]
4 Finde den Radius von der Oberfläche. Verwende die Formel r = √ (A / (4π)). Die Oberfläche einer Kugel ergibt sich aus der Gleichung A = 4πr2. Das Auflösen für die r-Variable ergibt √ (A / (4π)) = r, was bedeutet, dass der Radius einer Kugel gleich der Quadratwurzel der Oberfläche dividiert durch 4π ist. Sie können auch (A / (4π)) für das gleiche Ergebnis auf die halbe Potenz bringen.[5] - Wenn Sie eine Kugel mit einer Fläche von 1.200 cm haben2, löse den Radius wie folgt:
- √ (A / (4π)) = r
- √ (1200 / (4π)) = r
- √ (300 / (π)) = r
- √ (95.49) = r
- 9,77 cm = r
- Wenn Sie eine Kugel mit einer Fläche von 1.200 cm haben2, löse den Radius wie folgt:
Methode zwei von drei:
Schlüsselkonzepte definieren
-
 1 Identifizieren Sie die grundlegenden Maße einer Kugel. Der Radius (r) ist der Abstand vom exakten Mittelpunkt der Kugel zu einem beliebigen Punkt auf der Kugeloberfläche. Im Allgemeinen können Sie den Radius einer Kugel finden, wenn Sie den Durchmesser, den Umfang, das Volumen oder die Oberfläche kennen.
1 Identifizieren Sie die grundlegenden Maße einer Kugel. Der Radius (r) ist der Abstand vom exakten Mittelpunkt der Kugel zu einem beliebigen Punkt auf der Kugeloberfläche. Im Allgemeinen können Sie den Radius einer Kugel finden, wenn Sie den Durchmesser, den Umfang, das Volumen oder die Oberfläche kennen. - Durchmesser (D): die Entfernung über die Kugel - den Radius verdoppeln. Durchmesser ist die Länge einer Linie durch den Mittelpunkt der Kugel: von einem Punkt auf der Außenseite der Kugel zu einem entsprechenden Punkt direkt gegenüber. Mit anderen Worten, der größtmögliche Abstand zwischen zwei Punkten auf der Kugel.
- Umfang (C): der eindimensionale Abstand um die Kugel an ihrer breitesten Stelle. Mit anderen Worten, der Umfang eines kugelförmigen Querschnitts, dessen Ebene durch das Zentrum der Kugel verläuft.
- Volumen (V): der dreidimensionale Raum, der in der Kugel enthalten ist. Es ist der "Raum, den die Sphäre einnimmt".[6]
- Oberfläche (A): der zweidimensionale Bereich auf der äußeren Oberfläche der Kugel. Die Menge an flachem Raum, die die Außenseite der Kugel abdeckt.
- Pi (π): eine Konstante, die das Verhältnis des Kreisumfangs zum Kreisdurchmesser ausdrückt. Die ersten zehn Ziffern von Pi sind immer 3.141592653, obwohl es normalerweise gerundet wird 3.14.
-
 2 Verwenden Sie verschiedene Messungen, um den Radius zu finden. Sie können den Durchmesser, den Umfang, das Volumen und die Fläche verwenden, um den Radius einer Kugel zu berechnen. Sie können auch jede dieser Zahlen berechnen, wenn Sie die Länge des Radius selbst kennen. Versuchen Sie daher, die Formeln für die Berechnungen dieser Komponenten umzukehren, um den Radius zu finden. Lerne die Formeln, die den Radius verwenden, um Durchmesser, Umfang, Volumen und Oberfläche zu finden.
2 Verwenden Sie verschiedene Messungen, um den Radius zu finden. Sie können den Durchmesser, den Umfang, das Volumen und die Fläche verwenden, um den Radius einer Kugel zu berechnen. Sie können auch jede dieser Zahlen berechnen, wenn Sie die Länge des Radius selbst kennen. Versuchen Sie daher, die Formeln für die Berechnungen dieser Komponenten umzukehren, um den Radius zu finden. Lerne die Formeln, die den Radius verwenden, um Durchmesser, Umfang, Volumen und Oberfläche zu finden. - D = 2r. Wie bei Kreisen ist der Durchmesser einer Kugel doppelt so groß wie der Radius.
- C = πD oder 2πr. Wie bei Kreisen ist der Umfang einer Kugel gleich dem π-fachen des Durchmessers. Da der Durchmesser das Doppelte des Radius ist, können wir auch sagen, dass der Umfang das Doppelte des Radius mal π ist.
- V = (4/3) πr3. Das Volumen einer Kugel ist der Radius gewürfelt (mal selbst zweimal), mal π, mal 4/3.[7]
- A = 4πr2. Die Fläche einer Kugel ist der Radius im Quadrat (mal selbst), mal π, mal 4. Da die Fläche eines Kreises πr ist2Man kann auch sagen, dass die Oberfläche einer Kugel das Vierfache der Fläche des Kreises ist, der durch ihren Umfang gebildet wird.
Methode drei von drei:
Den Radius als Abstand zwischen zwei Punkten finden
-
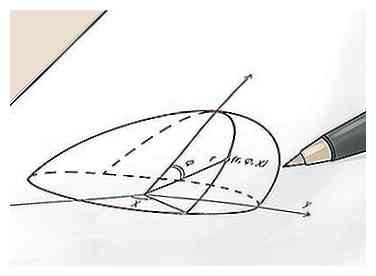 1 Finde die (x, y, z) -Koordinaten des Mittelpunkts der Kugel. Eine Möglichkeit, an den Radius einer Kugel zu denken, ist der Abstand zwischen dem Punkt in der Mitte der Kugel und einem beliebigen Punkt auf der Kugeloberfläche. Weil das wahr ist, wenn Sie die Koordinaten des Punktes in der Mitte der Kugel und eines beliebigen Punktes auf der Oberfläche kennen, können Sie den Radius der Kugel einfach dadurch finden, dass Sie den Abstand zwischen den zwei Punkten mit einer Variante der Basis berechnen Distanzformel. Suchen Sie zunächst nach den Koordinaten des Mittelpunkts der Kugel. Beachten Sie, dass, weil Kugeln dreidimensional sind, dies ein Punkt (x, y, z) und nicht ein (x, y) Punkt ist.
1 Finde die (x, y, z) -Koordinaten des Mittelpunkts der Kugel. Eine Möglichkeit, an den Radius einer Kugel zu denken, ist der Abstand zwischen dem Punkt in der Mitte der Kugel und einem beliebigen Punkt auf der Kugeloberfläche. Weil das wahr ist, wenn Sie die Koordinaten des Punktes in der Mitte der Kugel und eines beliebigen Punktes auf der Oberfläche kennen, können Sie den Radius der Kugel einfach dadurch finden, dass Sie den Abstand zwischen den zwei Punkten mit einer Variante der Basis berechnen Distanzformel. Suchen Sie zunächst nach den Koordinaten des Mittelpunkts der Kugel. Beachten Sie, dass, weil Kugeln dreidimensional sind, dies ein Punkt (x, y, z) und nicht ein (x, y) Punkt ist. - Dieser Prozess ist einfacher zu verstehen, wenn Sie einem Beispiel folgen. Für unsere Zwecke sagen wir, dass wir eine Kugel haben, die um den Punkt (x, y, z) zentriert ist (4, -1, 12). In den nächsten Schritten werden wir diesen Punkt verwenden, um den Radius zu finden.
-
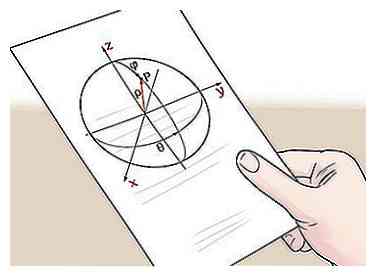 2 Finde die Koordinaten eines Punktes auf der Oberfläche der Kugel. Als nächstes müssen Sie die (x, y, z) Koordinaten eines Punktes auf der Oberfläche der Kugel finden. Das kann sein irgendein zeigen Sie auf die Oberfläche der Kugel. Da die Punkte auf der Oberfläche einer Kugel definitionsgemäß vom Mittelpunkt gleich weit entfernt sind, funktioniert jeder Punkt zur Bestimmung des Radius.
2 Finde die Koordinaten eines Punktes auf der Oberfläche der Kugel. Als nächstes müssen Sie die (x, y, z) Koordinaten eines Punktes auf der Oberfläche der Kugel finden. Das kann sein irgendein zeigen Sie auf die Oberfläche der Kugel. Da die Punkte auf der Oberfläche einer Kugel definitionsgemäß vom Mittelpunkt gleich weit entfernt sind, funktioniert jeder Punkt zur Bestimmung des Radius. - Im Sinne unseres Beispielproblems wollen wir sagen, dass wir diesen Punkt kennen (3, 3, 0) liegt auf der Oberfläche der Kugel. Indem wir den Abstand zwischen diesem Punkt und dem Mittelpunkt berechnen, können wir den Radius finden.
-
 3 Finde den Radius mit der Formel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Jetzt, da Sie das Zentrum der Kugel und einen Punkt auf der Oberfläche kennen, wird die Berechnung des Abstands zwischen den beiden den Radius finden. Verwenden Sie die dreidimensionale Abstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), wobei d gleich der Entfernung ist, (x1, y1z1) ist gleich den Koordinaten des Mittelpunkts und (x2, y2z2) entspricht den Koordinaten des Punktes auf der Oberfläche, um den Abstand zwischen den beiden Punkten zu finden.
3 Finde den Radius mit der Formel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Jetzt, da Sie das Zentrum der Kugel und einen Punkt auf der Oberfläche kennen, wird die Berechnung des Abstands zwischen den beiden den Radius finden. Verwenden Sie die dreidimensionale Abstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), wobei d gleich der Entfernung ist, (x1, y1z1) ist gleich den Koordinaten des Mittelpunkts und (x2, y2z2) entspricht den Koordinaten des Punktes auf der Oberfläche, um den Abstand zwischen den beiden Punkten zu finden. - In unserem Beispiel würden wir (4, -1, 12) für (x1, y1z1) und (3, 3, 0) für (x2, y2z2), lösen wie folgt:
- d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2)
- d = √ ((3 - 4)2 + (3 - -1)2 + (0 - 12)2)
- d = √ ((- 1)2 + (4)2 + (-12)2)
- d = √ (1 + 16 + 144)
- d = √ (161)
- d = 12,69. Dies ist der Radius unserer Sphäre.
- In unserem Beispiel würden wir (4, -1, 12) für (x1, y1z1) und (3, 3, 0) für (x2, y2z2), lösen wie folgt:
-
 4 Wissen, dass in allgemeinen Fällen r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). In einer Kugel ist jeder Punkt auf der Kugeloberfläche gleich weit vom Mittelpunkt entfernt. Wenn wir die obige dreidimensionale Abstandsformel nehmen und die Variable "d" durch die Variable "r" für den Radius ersetzen, erhalten wir eine Form der Gleichung, die den Radius eines beliebigen Mittelpunkts (x1, y1z1) und einem entsprechenden Oberflächenpunkt (x2, y2z2).
4 Wissen, dass in allgemeinen Fällen r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). In einer Kugel ist jeder Punkt auf der Kugeloberfläche gleich weit vom Mittelpunkt entfernt. Wenn wir die obige dreidimensionale Abstandsformel nehmen und die Variable "d" durch die Variable "r" für den Radius ersetzen, erhalten wir eine Form der Gleichung, die den Radius eines beliebigen Mittelpunkts (x1, y1z1) und einem entsprechenden Oberflächenpunkt (x2, y2z2). - Indem wir beide Seiten dieser Gleichung quadrieren, erhalten wir r2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2. Beachten Sie, dass dies im Wesentlichen gleich der Grundkugelgleichung r ist2 = x2 + y2 + z2 was einen Mittelpunkt von (0,0,0) annimmt.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Finde den Radius, wenn du den Durchmesser kennst. Der Radius ist der halbe Durchmesser. Verwenden Sie die Formel r = D / 2. Dies ist identisch mit der Methode, mit der der Radius eines Kreises aus seinem Durchmesser berechnet wird.[1]
1 Finde den Radius, wenn du den Durchmesser kennst. Der Radius ist der halbe Durchmesser. Verwenden Sie die Formel r = D / 2. Dies ist identisch mit der Methode, mit der der Radius eines Kreises aus seinem Durchmesser berechnet wird.[1]  2 Finde den Radius, wenn du den Umfang kennst. Verwende die Formel C / 2 & pgr ;.. Da der Umfang gleich πD ist, was gleich 2πr ist, ergibt die Division des Umfangs durch 2π den Radius.[2]
2 Finde den Radius, wenn du den Umfang kennst. Verwende die Formel C / 2 & pgr ;.. Da der Umfang gleich πD ist, was gleich 2πr ist, ergibt die Division des Umfangs durch 2π den Radius.[2] 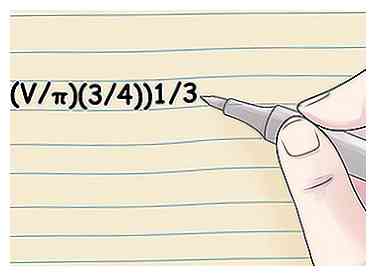 3 Berechnen Sie den Radius, wenn Sie das Volumen einer Kugel kennen. Benutze die Formel ((V / π) (3/4))1/3.[3] Das Volumen einer Kugel ergibt sich aus der Gleichung V = (4/3) πr3. Die Lösung für die r-Variable in dieser Gleichung erhält ((V / π) (3/4))1/3 = r, was bedeutet, dass der Radius einer Kugel gleich dem Volumen dividiert durch π, mal 3/4 ist, alle zu der Potenz 1/3 (oder der Kubikwurzel).[4]
3 Berechnen Sie den Radius, wenn Sie das Volumen einer Kugel kennen. Benutze die Formel ((V / π) (3/4))1/3.[3] Das Volumen einer Kugel ergibt sich aus der Gleichung V = (4/3) πr3. Die Lösung für die r-Variable in dieser Gleichung erhält ((V / π) (3/4))1/3 = r, was bedeutet, dass der Radius einer Kugel gleich dem Volumen dividiert durch π, mal 3/4 ist, alle zu der Potenz 1/3 (oder der Kubikwurzel).[4]  4 Finde den Radius von der Oberfläche. Verwende die Formel r = √ (A / (4π)). Die Oberfläche einer Kugel ergibt sich aus der Gleichung A = 4πr2. Das Auflösen für die r-Variable ergibt √ (A / (4π)) = r, was bedeutet, dass der Radius einer Kugel gleich der Quadratwurzel der Oberfläche dividiert durch 4π ist. Sie können auch (A / (4π)) für das gleiche Ergebnis auf die halbe Potenz bringen.[5]
4 Finde den Radius von der Oberfläche. Verwende die Formel r = √ (A / (4π)). Die Oberfläche einer Kugel ergibt sich aus der Gleichung A = 4πr2. Das Auflösen für die r-Variable ergibt √ (A / (4π)) = r, was bedeutet, dass der Radius einer Kugel gleich der Quadratwurzel der Oberfläche dividiert durch 4π ist. Sie können auch (A / (4π)) für das gleiche Ergebnis auf die halbe Potenz bringen.[5]  1 Identifizieren Sie die grundlegenden Maße einer Kugel. Der Radius (r) ist der Abstand vom exakten Mittelpunkt der Kugel zu einem beliebigen Punkt auf der Kugeloberfläche. Im Allgemeinen können Sie den Radius einer Kugel finden, wenn Sie den Durchmesser, den Umfang, das Volumen oder die Oberfläche kennen.
1 Identifizieren Sie die grundlegenden Maße einer Kugel. Der Radius (r) ist der Abstand vom exakten Mittelpunkt der Kugel zu einem beliebigen Punkt auf der Kugeloberfläche. Im Allgemeinen können Sie den Radius einer Kugel finden, wenn Sie den Durchmesser, den Umfang, das Volumen oder die Oberfläche kennen.  2 Verwenden Sie verschiedene Messungen, um den Radius zu finden. Sie können den Durchmesser, den Umfang, das Volumen und die Fläche verwenden, um den Radius einer Kugel zu berechnen. Sie können auch jede dieser Zahlen berechnen, wenn Sie die Länge des Radius selbst kennen. Versuchen Sie daher, die Formeln für die Berechnungen dieser Komponenten umzukehren, um den Radius zu finden. Lerne die Formeln, die den Radius verwenden, um Durchmesser, Umfang, Volumen und Oberfläche zu finden.
2 Verwenden Sie verschiedene Messungen, um den Radius zu finden. Sie können den Durchmesser, den Umfang, das Volumen und die Fläche verwenden, um den Radius einer Kugel zu berechnen. Sie können auch jede dieser Zahlen berechnen, wenn Sie die Länge des Radius selbst kennen. Versuchen Sie daher, die Formeln für die Berechnungen dieser Komponenten umzukehren, um den Radius zu finden. Lerne die Formeln, die den Radius verwenden, um Durchmesser, Umfang, Volumen und Oberfläche zu finden.  1 Finde die (x, y, z) -Koordinaten des Mittelpunkts der Kugel. Eine Möglichkeit, an den Radius einer Kugel zu denken, ist der Abstand zwischen dem Punkt in der Mitte der Kugel und einem beliebigen Punkt auf der Kugeloberfläche. Weil das wahr ist, wenn Sie die Koordinaten des Punktes in der Mitte der Kugel und eines beliebigen Punktes auf der Oberfläche kennen, können Sie den Radius der Kugel einfach dadurch finden, dass Sie den Abstand zwischen den zwei Punkten mit einer Variante der Basis berechnen Distanzformel. Suchen Sie zunächst nach den Koordinaten des Mittelpunkts der Kugel. Beachten Sie, dass, weil Kugeln dreidimensional sind, dies ein Punkt (x, y, z) und nicht ein (x, y) Punkt ist.
1 Finde die (x, y, z) -Koordinaten des Mittelpunkts der Kugel. Eine Möglichkeit, an den Radius einer Kugel zu denken, ist der Abstand zwischen dem Punkt in der Mitte der Kugel und einem beliebigen Punkt auf der Kugeloberfläche. Weil das wahr ist, wenn Sie die Koordinaten des Punktes in der Mitte der Kugel und eines beliebigen Punktes auf der Oberfläche kennen, können Sie den Radius der Kugel einfach dadurch finden, dass Sie den Abstand zwischen den zwei Punkten mit einer Variante der Basis berechnen Distanzformel. Suchen Sie zunächst nach den Koordinaten des Mittelpunkts der Kugel. Beachten Sie, dass, weil Kugeln dreidimensional sind, dies ein Punkt (x, y, z) und nicht ein (x, y) Punkt ist.  2 Finde die Koordinaten eines Punktes auf der Oberfläche der Kugel. Als nächstes müssen Sie die (x, y, z) Koordinaten eines Punktes auf der Oberfläche der Kugel finden. Das kann sein irgendein zeigen Sie auf die Oberfläche der Kugel. Da die Punkte auf der Oberfläche einer Kugel definitionsgemäß vom Mittelpunkt gleich weit entfernt sind, funktioniert jeder Punkt zur Bestimmung des Radius.
2 Finde die Koordinaten eines Punktes auf der Oberfläche der Kugel. Als nächstes müssen Sie die (x, y, z) Koordinaten eines Punktes auf der Oberfläche der Kugel finden. Das kann sein irgendein zeigen Sie auf die Oberfläche der Kugel. Da die Punkte auf der Oberfläche einer Kugel definitionsgemäß vom Mittelpunkt gleich weit entfernt sind, funktioniert jeder Punkt zur Bestimmung des Radius.  3 Finde den Radius mit der Formel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Jetzt, da Sie das Zentrum der Kugel und einen Punkt auf der Oberfläche kennen, wird die Berechnung des Abstands zwischen den beiden den Radius finden. Verwenden Sie die dreidimensionale Abstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), wobei d gleich der Entfernung ist, (x1, y1z1) ist gleich den Koordinaten des Mittelpunkts und (x2, y2z2) entspricht den Koordinaten des Punktes auf der Oberfläche, um den Abstand zwischen den beiden Punkten zu finden.
3 Finde den Radius mit der Formel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Jetzt, da Sie das Zentrum der Kugel und einen Punkt auf der Oberfläche kennen, wird die Berechnung des Abstands zwischen den beiden den Radius finden. Verwenden Sie die dreidimensionale Abstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), wobei d gleich der Entfernung ist, (x1, y1z1) ist gleich den Koordinaten des Mittelpunkts und (x2, y2z2) entspricht den Koordinaten des Punktes auf der Oberfläche, um den Abstand zwischen den beiden Punkten zu finden.  4 Wissen, dass in allgemeinen Fällen r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). In einer Kugel ist jeder Punkt auf der Kugeloberfläche gleich weit vom Mittelpunkt entfernt. Wenn wir die obige dreidimensionale Abstandsformel nehmen und die Variable "d" durch die Variable "r" für den Radius ersetzen, erhalten wir eine Form der Gleichung, die den Radius eines beliebigen Mittelpunkts (x1, y1z1) und einem entsprechenden Oberflächenpunkt (x2, y2z2).
4 Wissen, dass in allgemeinen Fällen r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). In einer Kugel ist jeder Punkt auf der Kugeloberfläche gleich weit vom Mittelpunkt entfernt. Wenn wir die obige dreidimensionale Abstandsformel nehmen und die Variable "d" durch die Variable "r" für den Radius ersetzen, erhalten wir eine Form der Gleichung, die den Radius eines beliebigen Mittelpunkts (x1, y1z1) und einem entsprechenden Oberflächenpunkt (x2, y2z2).